Информатика
Тема 4
Программирование на C++: алгоритмы поиска и сортировки. II
Агенда
- Алгоритмы и их сравнение
- Сортировка выбором
- Быстрая сортировка
Алгоритмы и их сравнение
Алгоритм — метод решения задачи, пригодный для реализации в виде компьютерной программы
Алгоритмы сравнивают по времени и памяти
| Линейный поиск | Бинарный поиск | |
|---|---|---|
| Лучший случай | 1 | 1 |
| Худший случай | \(n\) | \(\log_2(n)\) |
| В среднем | \(n\) | \(\log_2(n)\) |
В таблице указано количество шагов (сравнений) алгоритмов поиска
Пример для среднего случая линейного поиска
- В массиве длины n искомый элемент может быть на одной из n позиций, либо отсутствовать
- Если искомый элемент на 1 позиции, то мы его найдём за 1 шаг
- Если искомый элемент на последней позиции, то мы его найдём за n шагов
- Для всех возможных вариантов суммарное число шагов (арифметическая прогрессия) \[ 1 + 2 + 3 + 4 + \dots + n = \frac{n(n+1)}{2} \]
- Если искомый элемент отсутствует, то мы это поймём за \(n\) шагов
Пример для среднего случая линейного поиска
- Для всех возможных вариантов мы имеем суммарное число шагов \[ \frac{n(n+1)}{2} + n \]
- В среднем необходимо число шагов \[ \frac{n(n+1)/2 + n}{n} = \frac{n}{2}+\frac{1}{2} + 1 \]
- Для больших массивов \[ \approx n \]
\(O\)-нотация
Функция \(g(n)\) является \(O(f(n))\), если существуют такие постоянные \(c_0\) и \(n_0\), что \(g(n) < c_0 f(n)\) для всех \(n > n_0\)
Другими словами: при достаточно больших \(n\) функция \(g(n)\) растёт медленнее \(f(n)\)
\(O\)-нотация
| Сложение | \(O(f_1) + O(f_2) = O(\max(f_1,f_2))\) |
| Умножение | \(O(f_1)O(f_2) = O(f_1 f_2)\) |
| Умножение на константу | \(O(|k| f) = O(f)\) |
\(O\)-нотация используется для описания асимптотических выражений*, которые используются для оценки вычислительной сложности алгоритмов
*выражения для больших \(n\)
Пример
\[ \frac{n(n+1)/2 + n}{n} = O(n) \]
Распространённые виды вычислительной сложности
| Константная | \(O(1)\) |
| Логарифмическая | \(O(\log(n))\) |
| Линейная | \(O(n)\) |
| Линейно-логарифмическая | \(O(n\log(n))\) |
| Квадратичная | \(O(n^2)\) |
| Экспоненциальная | \(O(2^n)\) |
Разделяй и властвуй
Метод решения задач, в котором исходная задача делится на меньшие подзадачи
Решение в 3 шага:
- Разбиваем задачу на подзадачи
- Решаем подзадачи
- Объединяем решения подзадач
Основная теорема о рекуррентных соотношениях
\[ T(n) = a T\left(\frac{n}{b}\right) + O(n^d) \]
\[ a \ge 1, b > 1 \]
\(a\) — количество подзадач, \(b\) — во сколько раз уменьшается подзадача, \(T\) — время вычисления, \(d\) — показатель экспоненты оценки сложности выполнения нерекурсивной части
Основная теорема о рекуррентных соотношениях
| Если \(a=b^d\) | \(T(n)=O(n^d \log(n))\) |
| Если \(a < b^d\) | \(T(n)=O(n^d)\) |
| Если \(a>b^d\) | \(T(n)=O(n^{\log_b a})\) |
Пример
Для бинарного поиска \(a=1\), \(b=2\), \(d=0\), то есть \(1 = 2^0\) (первый случай), следовательно асимптотическая оценка вычислительной сложность бинарного поиска \(O(n^0 \log(n)) = O(\log(n)) \)

Сортировка выбором
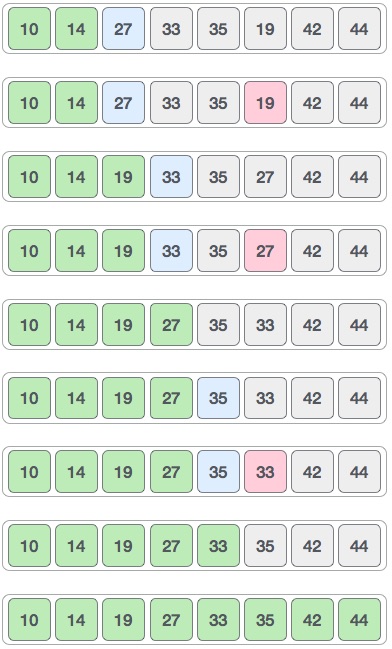
Визуализация сортировки
Быстрая сортировка